Research
Our group studies transport and dynamics in quantum many-body systems. We are especially interested in the combined effects of disorder and interactions in low-dimensional systems. Prominent examples are the two-dimensional electron liquid near the metal-insulator transition and disordered superconducting films near the transition to the superconducting state. We are also engaged in research on systems with strong spin-orbit coupling such as topological insulators and in aspects of spintronics. Most of our studies are based on methods of quantum field theory in condensed matter physics.
We gratefully acknowledge funding by the National Science Foundation (NSF) under Grant No. DMR-1742752.
Recent highlights

In this article prepared for the second edition of the Encyclopedia of Condensed Matter Physics (Elsevier), we review theoretical aspects of the disordered electron liquid with interaction. The physics of itinerant electrons is governed by the combined effect of disorder and 𝑒-𝑒 interactions. Such systems display singular corrections in transport and thermodynamics and can be described in terms of a scale-dependent Fermi liquid. The metal-insulator transition (MIT) arising in disordered systems in the presence of interactions is a non-trivial example of a quantum phase transition. The dynamical exponent characterizing this transition is determined by a special renormalization group equation. In two dimensions, the MIT can be discussed in terms of a flow in the disorder-interaction phase plane. As far as thermal transport is concerned, the Wiedemann-Franz law holds for short range interactions, but is violated by the long-range Coulomb interactions. Reference: A. M. Finkel'stein and G. Schwiete, Disordered electron liquid with interactions: theoretical aspects, Encyclopedia of Condensed Matter Physics, 2nd edition, Volume 3, pages 220-235 (2024). Link: doi.org/10.1016/B978-0-323-90800-9.00078-0
We review the scaling theory of disordered itinerant electrons with interactions. We first show how to adjust the microscopic Fermi-liquid theory to the presence of disorder. Then we describe the non-linear sigma model (NLSM) with interactions (Finkel’stein’s model). This model is closely connected to the Fermi liquid, but is more generally applicable, since it can also be viewed as a minimal effective functional describing disordered interacting electrons. Our discussion emphasizes the general structure of the theory, and the connection of the scaling parameters to conservation laws. We then move on to discuss the metal–insulator transition (MIT) in the disordered electron liquid in two and three dimensions. Generally speaking, this MIT is a non-trivial example of a quantum phase transition. The NLSM approach allows to identify the dynamical exponent connecting the spatial and energy scales, which is central for the description of the kinetic and thermodynamic behavior of the system in the critical region of the MIT in three dimensions. In two dimensions, the system can be discussed in terms of a flow in the disorder-interaction phase plane, which is controlled by a fixed point. We demonstrate that the two-parameter RG-equations accurately describe electrons in Si-MOSFETs including the observed non-monotonic behavior of the resistance and its strong drop at low temperatures. The theory can also be applied to systems with an attractive interaction in the Cooper channel, where it describes the suppression of superconductivity in disordered amorphous films. We extend our discussion to heat transport in the two-dimensional electron liquid. Similar to the electric conductivity, the thermal conductivity also acquires logarithmic corrections induced by the interplay of the electron interaction and disorder. The resulting thermal conductivity can be calculated in the NLSM formalism after introducing so-called gravitational potentials. It may be concluded that the combined effect of disorder and interactions determines all aspects of the physics of itinerant electrons in the presence of disorder. Reference: Scale-dependent theory of the disordered electron liquid, Ann. Phys. 456, 169260 (2023). Link: doi.org/10.1016/j.aop.2023.169260.
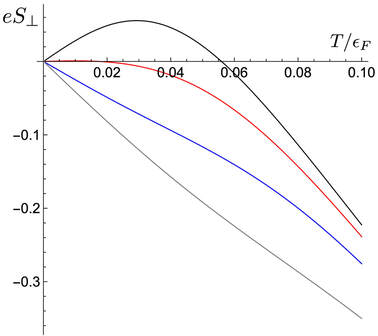
At low temperatures, the transport coefficients in the disordered electron gas acquire quantum corrections as a result of the complex interplay of disorder and interactions. The interaction corrections to the electric conductivity have their origin in virtual processes with typical electronic energies far exceeding the temperature. Here, we study interaction corrections δS to the thermopower S of the two-dimensional disordered electron gas with long-range Coulomb interactions. We show that while both real and virtual processes contribute to these corrections, the real processes are dominant and lead to a logarithmic temperature dependence of δS/S with δS/S<0. Reference: Z. I. Jitu and G. Schwiete, Interaction corrections to the thermopower of the disordered two-dimensional electron gas, preprint arXiv:2209.03995 (2022).
We study mesoscopic fluctuations in the supercurrent of a Josephson junction consisting of a topological insulator microbridge between two conventional superconductors. In the model, we account for the strong proximity effect when superconductors induce a gap in the spectrum of surface states as well as a magnetic field piercing the junction area that causes depairing and gap filling. The overall magnitude and functional form of the Josephson current fluctuations are determined by a combination of analytical and numerical methods, and found to sensitively depend on the coupling strength to surface states, Thouless energy, and pair-breaking energy scales in the problem. We also study the density of states that can be measured by scanning probes. Technically, mesoscopic fluctuations on top of the mean field description of the proximity effect in the topological region are described by a field theory approach, the replica nonlinear sigma-model in the class-D of the extended symmetry classification. Reference: M. Marinho, G. Vieira, T. Micklitz, G. Schwiete, and A. Levchenko, Mesoscopic fluctuations in superconductor-topological insulator Josephson junctions, Ann. Phys. (2022).
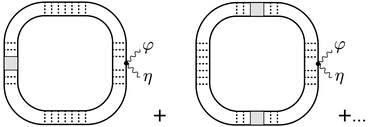
The non-linear sigma model is a well-established theoretical tool for studies of transport and thermodynamics in disordered electronic systems. The conventional sigma model approach for interacting systems does not account for particle-hole asymmetry. It is therefore not suited for studying quantities that are sensitive to this effect such as the thermoelectric transport coefficient. Here, we derive a minimal extension of the Keldysh non-linear sigma model tailored for two-dimensional interacting systems. We argue that this model can be used to systematically study the combined effect of interactions and disorder on thermoelectric transport. As a first step in this direction, we use the model to analyze the structure of the heat density-density correlation function and calculate interaction corrections to its static part. Reference: G. Schwiete, Nonlinear sigma model with particle-hole asymmetry for the disordered two-dimensional electron gas, Phys. Rev. B 103, 125422 (2021).
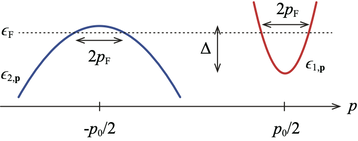
The Lorenz ratio serves as a measure to compare thermal and electric conductivities of metals. Recent experiments observed small Lorenz ratios in the compensated metal WP2, indicating that charge flow is strongly favored over heat conduction. Motivated by these findings, we study transport properties of compensated metals in the presence of electron-electron collisions and electron-impurity scattering. We focus on intermediate temperatures, where the phonon contributions to transport are weak and elastic and inelastic scattering rates are comparable. We find that the Lorenz ratio develops a temperature dependence as well as gets enhanced as a consequence of disorder scattering. For collisions mediated by the Coulomb interaction, impurities give rise to a non-monotonic dependence of the Lorenz ratio on the screening wave number with a minimum for intermediate screening strength. We also provide simple phenomenological expressions for the transport coefficients that allow for a physically transparent interpretation of the results. Reference: W.-R. Lee, K. Michaeli, and G. Schwiete, Lorenz ratio of an impure compensated metal in the degenerate Fermi liquid regime, accepted for publication in Phys. Rev. B (2021)
We discuss galvanomagnetic and thermomagnetic effects in disordered electronic systems focusing on intermediate temperatures, for which electron-electron scattering and electron-impurity scattering occur at similar rates, while phonon-related effects can be neglected. In particular, we explore how electric and thermal currents driven either by an electric field or by a temperature gradient are affected by the interplay of momentum-dependent electron-impurity scattering, electron-electron scattering, and the presence of a magnetic field. We find that the electric resistance, the Seebeck coefficient and the Nernst coefficient are particularly sensitive to the momentum dependence of the electron-impurity scattering rate at intermediate temperatures. A sufficiently strong momentum dependence of the electron-impurity scattering rate can induce a sign change of the Seebeck coefficient. This sign change can be suppressed by a perpendicular magnetic field. The temperature and magnetic field dependence of the Seebeck coefficient can be used for measuring the magnitude of the electron-impurity and electron-electron scattering rates. The Nernst coefficient vanishes for momentum-independent electron-impurity scattering but displays a maximum at finite temperatures once the momentum dependence is accounted for. By contrast, the Hall coefficient and the Righi-Leduc coefficient display only a weak dependence on the momentum dependence of the electron-impurity scattering at intermediate temperatures. Reference: W.-R. Lee, A. M. Finkel’stein, and G. Schwiete, Role of electron-electron collisions for magnetotransport at intermediate temperatures, Phys. Rev. B 102, 245117 (2020)
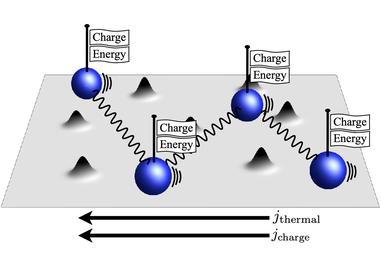
Electric, thermal, and thermoelectric transport in correlated electron systems probe different aspects of the many-body dynamics, and thus provide complementary information. These are well studied in the low- and high-temperature limits, while the experimentally important intermediate regime, in which elastic and inelastic scattering are both important, is less understood. To fill this gap, we provide comprehensive solutions of the Boltzmann equation in the presence of an electric field and a temperature gradient for two different cases: First, when electron-electron collisions are treated within the relaxation-time approximation while the full momentum dependence of electron-impurity scattering is included and, second, when the electron-impurity scattering is momentum independent, but the electron-electron collisions give rise to a momentum-dependent inelastic scattering rate of the Fermi-liquid type. We find that for Fermi-liquid as well as for Coulomb interactions, both methods give the same results for the leading temperature dependence of the transport coefficients. Moreover, the inelastic relaxation rate enters the electric conductivity and the Seebeck coefficient only when the momentum dependence of the electron-impurity collisions, analytical or nonanalytical, is included. Specifically, we show that inelastic processes only mildly affect the electric conductivity, but can generate a nonmonotonic dependence of the Seebeck coefficient on temperature and even a change of sign. Thermal conductivity, by contrast, always depends on the inelastic scattering rate even for a constant elastic relaxation rate. Reference: W.-R. Lee, A. M. Finkel’stein, K. Michaeli, and G. Schwiete, Role of electron-electron collisions for charge and heat transport at intermediate temperatures, Phys. Rev. Research 2, 013148 (2020)
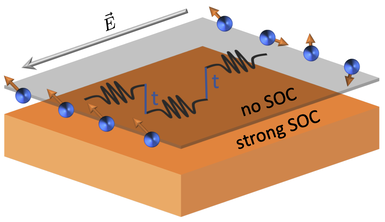
We study the electron and spin transport in a van der Waals system formed by one layer with strong spin- orbit coupling and a second layer without spin-orbit coupling, in the regime when the interlayer tunneling is random. We find that in the layer without intrinsic spin-orbit coupling, spin-charge coupled transport can be induced by two distinct mechanisms. First, the gapless diffusion modes of the two isolated layers hybridize in the presence of tunneling, which constitutes a source of spin-charge coupled transport in the second layer. Second, the random tunneling introduces spin-orbit coupling in the effective disorder-averaged single-particle Hamiltonian of the second layer. This results in nontrivial spin transport and, for sufficiently strong tunneling, in spin-charge coupling. As an example, we consider a van der Waals system formed by a two-dimensional electron gas (2DEG)—such as graphene—and the surface of a topological insulator (TI) and show that the proximity of the TI induces a coupling of the spin and charge transport in the 2DEG. In addition, we show that such coupling can be tuned by varying the doping of the TI’s surface. We then obtain, for a simple geometry, the current-induced nonequilibrium spin accumulation (Edelstein effect) caused in the 2DEG by the coupling of charge and spin transport. Reference: M. Rodriguez-Vega, G. Schwiete, and E. Rossi, Spin-charge coupled transport in van der Waals systems with random tunneling, Phys. Rev. Research 1, 033085 (2019)
Publications
A. M. Finkel’stein and G. Schwiete
Scale-dependent theory of the disordered electron liquid
Invited contribution to the Annals of Physics special issue “Correlations and Disorder” in memory of Konstantin Efetov
Annals of Physics 456, 169260 (2023)
Z. I. Jitu and G. Schwiete
Interaction corrections to the thermopower of the disordered two-dimensional electron gas
preprint: arXiv:2209.03995
A. M. Finkel'stein and G. Schwiete
Disordered electron liquid with interactions: theoretical aspects
Review article in the Encyclopedia of Condensed Matter Physics, 2nd edition, Elsevier (2023).
M. Marinho, G. Vieira, T. Micklitz, G. Schwiete, and A. Levchenko
Mesoscopic fluctuations in superconductor-topological insulator Josephson junctions
Annals of Physics 447, 168978 (2022)
G. Schwiete
Nonlinear sigma model with particle-hole asymmetry for the disordered two-dimensional electron gas
Phys. Rev. B 103, 125422 (2021)
W.-R. Lee, K. Michaeli, and G. Schwiete
Lorenz ratio of an impure compensated metal in the degenerate Fermi liquid regime
Phys. Rev. B 103, 115140 (2021)
W.-R. Lee, A. M. Finkel’stein, and G. Schwiete
Role of electron-electron collisions for magnetotransport at intermediate temperatures
Phys. Rev. B 102, 245117 (2020)
W.-R. Lee, A. M. Finkel’stein, K. Michaeli, and G. Schwiete
Role of electron-electron collisions for charge and heat transport at intermediate temperatures
Phys. Rev. Research 2, 013148 (2020)
M. Rodriguez-Vega, G. Schwiete, and E. Rossi
Spin-charge coupled transport in van der Waals systems with random tunneling
Phys. Rev. Research 1, 033085 (2019)
H. Velkov, G. N. Bremm, T. Micklitz, and G. Schwiete
Transport in topological insulators with bulk-surface coupling: Interference corrections and conductance fluctuations
Phys. Rev. B 98, 014406 (2018)
K. Yamamoto, O. Gomonay, J. Sinova, and G. Schwiete
Spin transfer torques and spin-dependent transport in a metallic F/AF/N tunneling junction
Phys. Rev. B 98, 014406 (2018)
M. Rodriguez-Vega, G. Schwiete, J. Sinova, and E. Rossi
Giant Edelstein effect in topological-insulator-graphene heterostructures
Phys. Rev. B 96, 235419 (2017)
H. Velkov, O. Gomonay, M. Beens, G. Schwiete, A. Brataas, J. Sinova, R. Duine
Phenomenology of current-driven skrymion motion in antiferromagnets
New J. Phys. 18, 075016 (2016)
G. Schwiete and A. M. Finkel’stein
Heat diffusion in the disordered electron gas with long-range Coulomb interactions
Phys. Rev. B 93, 115121 (2016)
G. Schwiete and A. M. Finkel’stein
Theory of Thermal Conductivity in the Disordered Electron Liquid
J. Exp. Theor. Phys. 122(3), 567 (2016)
G. Schwiete and A. M. Finkel’stein,
Renormalization group analysis of thermal transport in the disordered Fermi liquid
Phys. Rev. B 90, 155441 (2014)
G. Schwiete and A. M. Finkel’stein,
Thermal transport and the Wiedemann Franz law in the disordered Fermi liquid
Phys. Rev. B 90, 060201(R) (2014), Editor’s suggestion
G. Schwiete and A. M. Finkel’stein,
Keldysh approach to the renormalization group analysis of the disordered electron liquid
Phys. Rev. B 89, 075437 (2014)
G. Schwiete and A. M. Finkel’stein,
Kinetics of the disordered Bose gas with collisions
Phys. Rev. A 88, 053611 (2013)
B. Tarasinski and G. Schwiete,
Fluctuation conductivity of disordered superconductors in magnetic fields
Phys. Rev. B 88, 014518 (2013)
G. Schwiete and A. M. Finkel’stein,
Effective theory for the propagation of a wave-packet in a disordered and nonlinear medium
Phys. Rev. A 87, 043636 (2013)
M. Schneider, G. Schwiete, and P. W. Brouwer,
Semiclassical theory of interaction corrections to the conductance of antidot arrays
Phys. Rev. B 87, 195406 (2013)
K. S. Tikhonov, G. Schwiete, and A. M. Finkel’stein,
Fluctuation conductivity in disordered superconducting films
Phys. Rev. B 85, 174527 (2012)
G. Schwiete and Y. Oreg,
Fluctuation persistent current in small superconducting rings
Phys. Rev. B 82, 214514 (2010)
G. Schwiete and A. M. Finkel’stein,
Propagation of a wave-packet in the presence of disorder and nonlinearity,
Invited Article for the Review Volume: Perspectives of Mesoscopic Physics.
(World Scientific, Singapore, 2010), p. 249.
G. Schwiete and Y. Oreg,
Fluctuation persistent current and susceptibility in superconducting rings,
Invited Article for the Review Volume: Perspectives of Mesoscopic Physics.
(World Scientific, Singapore, 2010), p. 265.
G. Schwiete and A. M. Finkel’stein,
Nonlinear wave-packet dynamics in disordered media
Phys. Rev. Lett. 104, 103904 (2010)
G. Schwiete and Y. Oreg,
Persistent current in small superconducting rings
Phys. Rev. Lett. 103, 037001 (2009)
D. Greenbaum, S. Das, G. Schwiete, and P. G. Silvestrov,
Pure spin current in graphene NS structures
Phys. Rev. B 75, 195437 (2007)
G. Schwiete and K. B. Efetov,
Temperature dependence of the spin-susceptibility of a clean Fermi gas with repulsion Phys. Rev. B 74, 165108 (2006)
G. Schwiete and K. B. Efetov,
Supersymmetry for disordered systems with interaction
Phys. Rev. B 71, 134203 (2005)
I. S. Beloborodov, A. V. Lopatin, G. Schwiete and V. M. Vinokur,
Tunneling density of states of granular metals
Phys. Rev. B 70, 073404 (2004)
K. B. Efetov, G. Schwiete, and K. Takahashi,
Bosonization for disordered and chaotic systems
Phys. Rev. Lett. 92, 026807 (2004)
G. Schwiete, D. Taras-Semchuk, and K. B. Efetov,
Weak localization and integer quantum Hall effect in a periodic potential
Phys. Rev. B 67, 245319 (2003)
N. N. Nikolaev, W. Schäfer and G. Schwiete,
Coherent production of hard dijets on nuclei in QCD
Phys. Rev. D 63, 014020 (2001)
N. N. Nikolaev, W. Schäfer, and G. Schwiete,
Multiple-pomeron splitting in QCD - a novel antishadowing effect in coherent dijet production on nulcei
JETP Letters 72, 405 (2000)
G. Schwiete,
Higher order Coulomb corrections to the Primakoff measurement of the π0 lifetime
Acta Physica Polonica B 31, 10 (2000)
Scale-dependent theory of the disordered electron liquid
Invited contribution to the Annals of Physics special issue “Correlations and Disorder” in memory of Konstantin Efetov
Annals of Physics 456, 169260 (2023)
Z. I. Jitu and G. Schwiete
Interaction corrections to the thermopower of the disordered two-dimensional electron gas
preprint: arXiv:2209.03995
A. M. Finkel'stein and G. Schwiete
Disordered electron liquid with interactions: theoretical aspects
Review article in the Encyclopedia of Condensed Matter Physics, 2nd edition, Elsevier (2023).
M. Marinho, G. Vieira, T. Micklitz, G. Schwiete, and A. Levchenko
Mesoscopic fluctuations in superconductor-topological insulator Josephson junctions
Annals of Physics 447, 168978 (2022)
G. Schwiete
Nonlinear sigma model with particle-hole asymmetry for the disordered two-dimensional electron gas
Phys. Rev. B 103, 125422 (2021)
W.-R. Lee, K. Michaeli, and G. Schwiete
Lorenz ratio of an impure compensated metal in the degenerate Fermi liquid regime
Phys. Rev. B 103, 115140 (2021)
W.-R. Lee, A. M. Finkel’stein, and G. Schwiete
Role of electron-electron collisions for magnetotransport at intermediate temperatures
Phys. Rev. B 102, 245117 (2020)
W.-R. Lee, A. M. Finkel’stein, K. Michaeli, and G. Schwiete
Role of electron-electron collisions for charge and heat transport at intermediate temperatures
Phys. Rev. Research 2, 013148 (2020)
M. Rodriguez-Vega, G. Schwiete, and E. Rossi
Spin-charge coupled transport in van der Waals systems with random tunneling
Phys. Rev. Research 1, 033085 (2019)
H. Velkov, G. N. Bremm, T. Micklitz, and G. Schwiete
Transport in topological insulators with bulk-surface coupling: Interference corrections and conductance fluctuations
Phys. Rev. B 98, 014406 (2018)
K. Yamamoto, O. Gomonay, J. Sinova, and G. Schwiete
Spin transfer torques and spin-dependent transport in a metallic F/AF/N tunneling junction
Phys. Rev. B 98, 014406 (2018)
M. Rodriguez-Vega, G. Schwiete, J. Sinova, and E. Rossi
Giant Edelstein effect in topological-insulator-graphene heterostructures
Phys. Rev. B 96, 235419 (2017)
H. Velkov, O. Gomonay, M. Beens, G. Schwiete, A. Brataas, J. Sinova, R. Duine
Phenomenology of current-driven skrymion motion in antiferromagnets
New J. Phys. 18, 075016 (2016)
G. Schwiete and A. M. Finkel’stein
Heat diffusion in the disordered electron gas with long-range Coulomb interactions
Phys. Rev. B 93, 115121 (2016)
G. Schwiete and A. M. Finkel’stein
Theory of Thermal Conductivity in the Disordered Electron Liquid
J. Exp. Theor. Phys. 122(3), 567 (2016)
G. Schwiete and A. M. Finkel’stein,
Renormalization group analysis of thermal transport in the disordered Fermi liquid
Phys. Rev. B 90, 155441 (2014)
G. Schwiete and A. M. Finkel’stein,
Thermal transport and the Wiedemann Franz law in the disordered Fermi liquid
Phys. Rev. B 90, 060201(R) (2014), Editor’s suggestion
G. Schwiete and A. M. Finkel’stein,
Keldysh approach to the renormalization group analysis of the disordered electron liquid
Phys. Rev. B 89, 075437 (2014)
G. Schwiete and A. M. Finkel’stein,
Kinetics of the disordered Bose gas with collisions
Phys. Rev. A 88, 053611 (2013)
B. Tarasinski and G. Schwiete,
Fluctuation conductivity of disordered superconductors in magnetic fields
Phys. Rev. B 88, 014518 (2013)
G. Schwiete and A. M. Finkel’stein,
Effective theory for the propagation of a wave-packet in a disordered and nonlinear medium
Phys. Rev. A 87, 043636 (2013)
M. Schneider, G. Schwiete, and P. W. Brouwer,
Semiclassical theory of interaction corrections to the conductance of antidot arrays
Phys. Rev. B 87, 195406 (2013)
K. S. Tikhonov, G. Schwiete, and A. M. Finkel’stein,
Fluctuation conductivity in disordered superconducting films
Phys. Rev. B 85, 174527 (2012)
G. Schwiete and Y. Oreg,
Fluctuation persistent current in small superconducting rings
Phys. Rev. B 82, 214514 (2010)
G. Schwiete and A. M. Finkel’stein,
Propagation of a wave-packet in the presence of disorder and nonlinearity,
Invited Article for the Review Volume: Perspectives of Mesoscopic Physics.
(World Scientific, Singapore, 2010), p. 249.
G. Schwiete and Y. Oreg,
Fluctuation persistent current and susceptibility in superconducting rings,
Invited Article for the Review Volume: Perspectives of Mesoscopic Physics.
(World Scientific, Singapore, 2010), p. 265.
G. Schwiete and A. M. Finkel’stein,
Nonlinear wave-packet dynamics in disordered media
Phys. Rev. Lett. 104, 103904 (2010)
G. Schwiete and Y. Oreg,
Persistent current in small superconducting rings
Phys. Rev. Lett. 103, 037001 (2009)
D. Greenbaum, S. Das, G. Schwiete, and P. G. Silvestrov,
Pure spin current in graphene NS structures
Phys. Rev. B 75, 195437 (2007)
G. Schwiete and K. B. Efetov,
Temperature dependence of the spin-susceptibility of a clean Fermi gas with repulsion Phys. Rev. B 74, 165108 (2006)
G. Schwiete and K. B. Efetov,
Supersymmetry for disordered systems with interaction
Phys. Rev. B 71, 134203 (2005)
I. S. Beloborodov, A. V. Lopatin, G. Schwiete and V. M. Vinokur,
Tunneling density of states of granular metals
Phys. Rev. B 70, 073404 (2004)
K. B. Efetov, G. Schwiete, and K. Takahashi,
Bosonization for disordered and chaotic systems
Phys. Rev. Lett. 92, 026807 (2004)
G. Schwiete, D. Taras-Semchuk, and K. B. Efetov,
Weak localization and integer quantum Hall effect in a periodic potential
Phys. Rev. B 67, 245319 (2003)
N. N. Nikolaev, W. Schäfer and G. Schwiete,
Coherent production of hard dijets on nuclei in QCD
Phys. Rev. D 63, 014020 (2001)
N. N. Nikolaev, W. Schäfer, and G. Schwiete,
Multiple-pomeron splitting in QCD - a novel antishadowing effect in coherent dijet production on nulcei
JETP Letters 72, 405 (2000)
G. Schwiete,
Higher order Coulomb corrections to the Primakoff measurement of the π0 lifetime
Acta Physica Polonica B 31, 10 (2000)